简介
图表示点之间的关系,在C#中通过节点对象的集合来表示点(Vertex),用邻接矩阵(adjacency matrix)来表示点之间的关系。下面来看C#实现。
文章转载自:http://www.cnblogs.com/CareySon/archive/2012/04/20/2459447.html
表示点的对象
下面实现代码:
class Vertex
{
public string Data;
public bool IsVisited;
public Vertex(string Vertexdata)
{
Data = Vertexdata;
}
}每个节点包含两个字段,分别为节点数据以及表示是否被访问过的一个布尔类型。
表示图的对象
图中除了需要点的集合和邻接矩阵之外,还需要一些基本的向图中添加或删除元素的方法,以及一个构造方法来对图进行初始化。
public class Graph
{
//图中所能包含的点上限
private const int Number = 10;
//顶点数组
private Vertex[] vertiexes;
//邻接矩阵
public int[,] adjmatrix;
//统计当前图中有几个点
int numVerts = 0;
//初始化图
public Graph()
{
//初始化邻接矩阵和顶点数组
adjmatrix = new Int32[Number, Number];
vertiexes = new Vertex[Number];
//将代表邻接矩阵的表全初始化为0
for (int i = 0; i < Number; i++)
{
for (int j = 0; j < Number; j++)
{
adjmatrix[i, j] = 0;
}
}
}
//向图中添加节点
public void AddVertex(String v)
{
vertiexes[numVerts] = new Vertex(v);
numVerts++;
}
//向图中添加有向边
public void AddEdge(int vertex1, int vertex2)
{
adjmatrix[vertex1, vertex2] = 1;
//adjmatrix[vertex2, vertex1] = 1;
}
//显示点
public void DisplayVert(int vertexPosition)
{
Console.WriteLine(vertiexes[vertexPosition]+" ");
}
}拓扑排序(TopSort)
拓扑排序是对一个有向的,并且不是环路的图中所有的顶点线性化。需要如下几个步骤
1.首先找到没有后继的节点。
2.将这个节点加入线性栈中
3.在图中删除这个节点
4.重复步骤1,2,3
因此,首先需要找到后继节点的方法:
//寻找图中没有后继节点的点
//具体表现为邻接矩阵中某一列全为0
//此时返回行号,如果找不到返回-1
private int FindNoSuccessor()
{
bool isEdge;
//循环行
for (int i = 0; i < numVerts; i++)
{
isEdge = false;
//循环列,有一个1就跳出循环
for (int j = 0; j < numVerts; j++)
{
if (adjmatrix[i, j] == 1)
{
isEdge = true;
break;
}
}
if (!isEdge)
{
return i;
}
}
return -1;
}此外还需要删除图中点的方法,这个方法不仅需要删除图中对应位置的点,还需要删除邻接矩阵对应的行和列,因此设置了两个辅助方法,见代码。
//删除图中的点
//需要两个操作,分别从数组中删除点
//从邻接矩阵中消去被删点的行和列
private void DelVertex(int vert)
{
//保证不越界
if (vert <= numVerts - 1)
{
//删除节点
for (int i = vert; i < numVerts; i++)
{
vertiexes[i] = vertiexes[i + 1];
}
//删除邻接矩阵的行
for (int j = vert; j < numVerts; j++)
{
MoveRow(j, numVerts);
}
//删除邻接矩阵中的列,因为已经删了行,所以少一列
for (int k = vert; k < numVerts - 1;k++ )
{
MoveCol(k, numVerts-1);
}
//删除后减少一个
numVerts--;
}
}
//辅助方法,移动邻接矩阵中的行
private void MoveRow(int row, int length)
{
for (int col = row; col < numVerts; col++)
{
adjmatrix[row, col] = adjmatrix[row + 1, col];
}
}
//辅助方法,移动邻接矩阵中的列
private void MoveCol(int col, int length)
{
for (int row = col; row < numVerts; row++)
{
adjmatrix[row, col] = adjmatrix[row, col+1];
}
}有了这几个方法,就可以按照步骤开始拓扑排序了:
//拓扑排序
//找到没有后继节点的节点,删除,加入一个栈,然后输出
public void TopSort()
{
int origVerts = numVerts;
//存放返回节点的栈
System.Collections.Stack result = new Stack();
while (numVerts > 0)
{
//找到第一个没有后继节点的节点
int currVertex = FindNoSuccessor();
if (currVertex == -1)
{
Console.WriteLine("图为环路图,不能搞拓扑排序");
return;
}
//如果找到,将其加入返回结果栈
result.Push(vertiexes[currVertex].Data);
//然后删除此节点
DelVertex(currVertex);
}
/*输出排序后的结果*/
Console.Write("拓扑排序的顺序为:");
while (result.Count > 0)
{
Console.Write(result.Pop()+" ");
}
/*输出排序后的结果*/
}下面,对拓扑排序进行测试,代码如下:
static void Main(string[] args)
{
Graph g = new Graph();
g.AddVertex("A");
g.AddVertex("B");
g.AddVertex("C");
g.AddVertex("D");
g.AddEdge(0, 1);
g.AddEdge(1, 2);
g.AddEdge(2, 3);
g.AddEdge(3, 4);
g.TopSort();
Console.ReadKey();
}
测试结果:
图的遍历
很多时候,我们需要知道从图中给定点到另一个点是否能走通,比如几个车站之间是否可以连接。这时我们需要对图进行查找,查找大概可以分为两类,深度优先遍历和广度优先遍历,下面先来看深度优先遍历。
深度优先遍历(Depth-First Search)
深度优先遍历首先从一个点开始,到一条路径结束,然后循环找第二条路径,到结束,依此往复。
首先我们需要一个辅助方法返回给定的点最近一个连接并且未被访问过的序号。
//从邻接矩阵查找给定点第一个相邻且未被访问过的点
//参数v是给定点在邻接矩阵的行
private int GetAdjUnvisitedVertex(int v)
{
for (int j = 0; j < numVerts; j++)
{
if (adjmatrix[v,j]==1 && vertiexes[j].IsVisited == false)
{
return j;
}
}
return -1;
}
下面,就可以进行深度优先遍历了:
//深度优先遍历
public void DepthFirstSearch()
{
//声明一个存储临时结果的栈
System.Collections.Stack s = new Stack();
//先访问第一个节点
vertiexes[0].IsVisited = true;
DisplayVert(0);
s.Push(0);
int v;
while (s.Count > 0)
{
//获得和当前节点连接的未访问过节点的序号
v = GetAdjUnvisitedVertex((int)s.Peek());
if (v == -1)
{
s.Pop();
}
else
{
//标记为已经被访问过
vertiexes[v].IsVisited = true;
DisplayVert(v);
s.Push(v);
}
}
//重置所有节点为未访问过
for (int u = 0; u < numVerts; u++)
{
vertiexes[u].IsVisited = false;
}
}广度优先遍历(Breadth-First Search)
广度优先遍历首先遍历层级。算法如下:
//广度优先遍历
public void BreadthFirstSearch()
{
System.Collections.Queue q = new Queue();
/*首先访问第一个节点*/
vertiexes[0].IsVisited = true;
DisplayVert(0);
q.Enqueue(0);
/*第一个节点访问结束*/
int vert1, vert2;
while (q.Count > 0)
{
/*首先访问同层级第一个节点*/
vert1 = (int)q.Dequeue();
vert2 = GetAdjUnvisitedVertex(vert1);
/*结束*/
while (vert2 != -1)
{
/*首先访问第二个节点*/
vertiexes[vert2].IsVisited = true;
DisplayVert(vert2);
q.Enqueue(vert2);
//寻找邻接的
vert2 = GetAdjUnvisitedVertex(vert1);
}
}
//重置所有节点为未访问过
for (int u = 0; u < numVerts; u++)
{
vertiexes[u].IsVisited = false;
}
}
下面我们来测试深度优先和广度优先遍历:
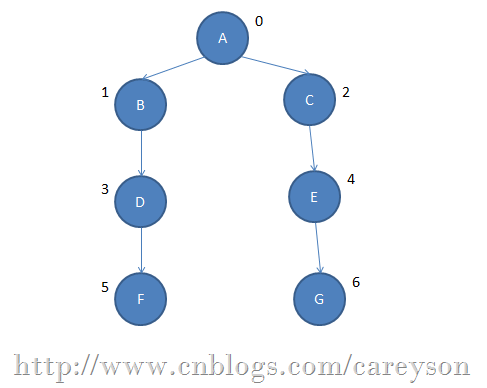
我们的测试生成一个如下的图:
测试代码:
static void Main(string[] args)
{
Graph g = new Graph();
g.AddVertex("A");
g.AddVertex("B");
g.AddVertex("C");
g.AddVertex("D");
g.AddVertex("E");
g.AddVertex("F");
g.AddVertex("G");
g.AddEdge(0, 1);
g.AddEdge(0, 2);
g.AddEdge(1, 3);
g.AddEdge(2, 4);
g.AddEdge(3, 5);
g.AddEdge(4, 6);
Console.WriteLine("n深度优先遍历");
g.DepthFirstSearch();
Console.WriteLine("n广度优先遍历");
g.BreadthFirstSearch();
Console.ReadKey();
}运行结果: