GN算法是一种分裂型的社区结构分裂算法。该算法根据网络中社区内部高内聚、社区之间低内聚的特点,逐步去除社区之间的边,取得相对内聚的社区结构。算法用边介数的概念来探测边的位置,某边的边介数定义为网络上所有顶点之间的最短路径通过该边的次数。由定义可知,如果一条边连接两个社区,那么这两个社团节点之间的最短路径通过该边的次数就会最多,相应的边介数最大。如果删除该边,那么两个社团就会分割开。GN算就就是基于此思想反复计算当前网络的最短路径,计算每条边的边介数,删除边介数最大的边。最后在一定条件下,算法停止,即可得到网络的社区结构。
以图1为例说明GN算法的执行流程。1.使用最短路径算法求在图1.a上求出顶点1到顶点8的最短路径(图中红色部分)。2.反复调用步骤1,探测网络所有顶点之间的最短路径,统计出所有边的边介数,如图1.b所示。3.统计出最大边介数,然后删除,得到如图1.c所示的社区结构。
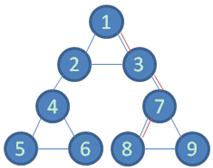
图1.a.最短路
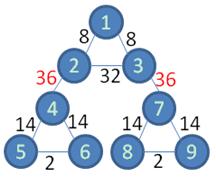
图1.b.边介数
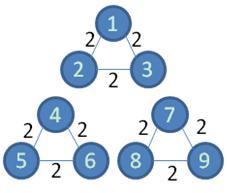
图1.c.删除最大边介数的边
实验数据来源于真实社会网络,提取石家庄铁道大学信息科学与技术学院2011级研究生在人人网的好友关系数据(二十人网络),整理后由UCINET分析软件分析本数据的一些基本特性,得出该网络凝聚系数为0.700,具有较高的内聚性。详细参数如图2所示。可视化该网络结构如图3所示。由图中看出该网络尚有4个孤立节点,该节点为未在人人网开设账户的同学,其存在不影响本算法的分析。
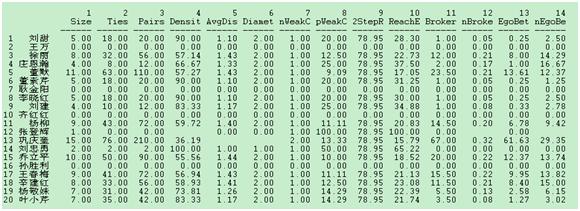
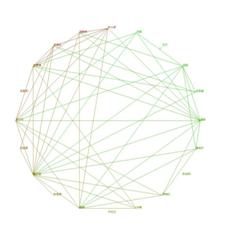
图3.实验数据可视化
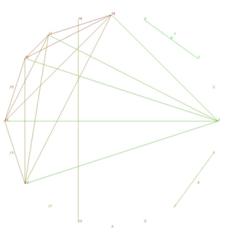
图4.子图数为11时的社区结构
数据改造成本程序的数据定义文件。程序采用文本形式存储网络的顶点和边定义。顶点定义为每行v order xposition yposition的形式,如v 1 251 636,表示顶点1位于X轴251,Y轴636处。边定义为每行a start end weight的形式,如a 1 2 34,表示从第一个顶点到第二个顶点的边,边的权重为34。
GN算法在本数据上测试。数据开始时,图的子图数subGraph为5,在经过N步求边介数、删边后,得出子图数subGraph为11的社区结构。其整体表现如图4所示。
从实验结果可以看出,该社会网络可以分解出一个内聚度更高的大社区和两个小社区,该大社区由6个顶点构成,这六个顶点之间联系最为紧密,节点是全连接的,同时顶点的边介数都为2。两个小社区均为两个顶点构成的。大社区六个顶点在原图中都是度较大的节点,这可以解释社会网络中活跃的用户之间联系的紧密性。两个小社区的成员都是具有高度相关性的节点构成的,节点对外联系较少,局部内聚性高,可以解释小团体的雏形。从删边过程中看,在前几步中求得的最大边介数点均为悬挂接点(只有一条边与整体网络连通的节点),该种节点高度依存与度较大的节点或与其连接的节点融入整体社区,其一般不参与构成社区。
使用GN算法可以较好的发现网络存在的社区结构,本算法对存在孤立节点的网络、全连接社区、无权图、高内聚网络等特殊形式,均表现出良好的鲁棒性。对于能否使用社区内部所有边的边介数相等来作为删边中止条件问题,小社区的存在前提和意义,以及悬挂节点在社区发现中的存在意义有待于进一步研究。
PS:感谢yangyangfuture指正该算法应属于分裂算法。
原文转载于:http://blog.sina.com.cn/s/blog_449a630601013cet.html