若干笔记……

今天加入苏苏的项目里面了。身为一个大水货……一头雾水听了项目介绍，就开始最基本的环境配置了……基本的要死。还是不会= =。

昨天在新买的二手电脑上装了WIN8.1，今天就因为项目软件的原因要换成win7 32位，可怜了我的8G内存。。。

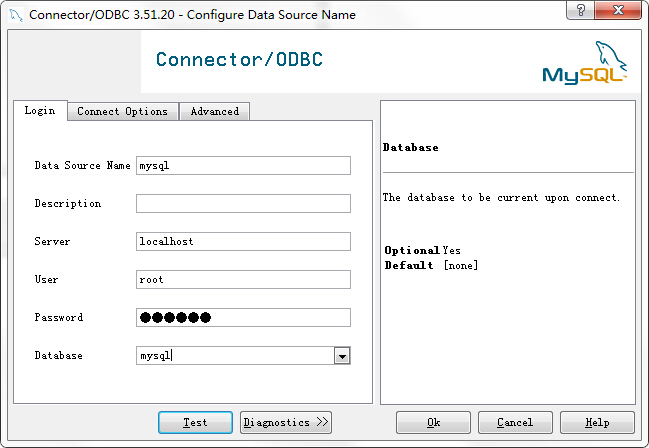
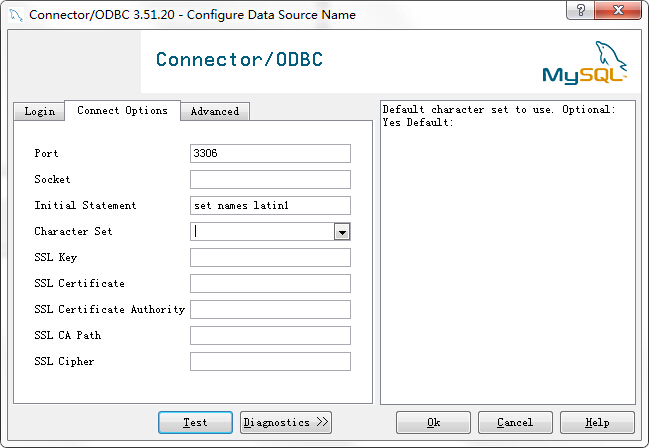
嗯。首先是用到了ODBC数据源管理器。应用程序要访问一个数据库，首先必须用ODBC管理器注册一个数据源，管理器根据数据源提供的数据库位置、数据库类型及ODBC驱动程序等信息，建立起ODBC与具体数据库的联系。这样，只要应用程序将数据源名提供给ODBC，ODBC就能建立起与相应数据库的连接。

具体的设置，就是打开ODBC数据源管理器。看是个人用了还是全用户用了，对于我这个个人电脑来说实际选哪个都无所谓，就选择系统DSN。然后添加，前提是装了MySQL数据库（这里使用的是南瑞专用的数据库），然后，添加的时候，选择MySQL ODBC 3.51 Driver 。如下图设置：

数据库给了一个压缩包，直接将db文件夹复制到mysql程序目录下的data目录中即可。跟以前的执行SQL语句方式不同……不过db上一层目录的那个文件中有一个FDB文件，应该是FirebirdDB数据库文件。

用到了两个插件，一个是形成Excel表格的插件，名字叫：Microsoft.Office.Interop.Excel，不过这个默认的时候，就可以直接引用。另外一个插件是MySQLDriverCS，需要另外安装。

MySQLDriverCS是MySQL数据库的一个免费开源的.NET驱动程序。和Sql .NET Data Provider是为Sql Server一样，它是专门为MySQL设计的，可以叫做MySQL .NET Data Provider。使用他不需要额外的去设置ODBC数据源，基本上只要能连接到MySQL就能通过MySQLDriverCS来访问。这个。没有测试不设置ODBC数据源是否能够访问。不过应该是可以的。。之前报错是因为一直没有安装插件的缘故。

另外百度百科上说明，这个只支持32位，不支持64位。

电力系统中限制短路电流的措施有：采用分裂绕组变压器、分裂电抗器、限流电抗器、变压器分列运行、环网解环运行等等

n-1原则（N-1准则）：判定电力系统安全性的一种准则。又称单一故障安全准则。按照这一准则,电力系统的N个元件中的任一独立元件（发电机、输电线路、变压器等）发生故障而被切除后，应不造成因其他线路过负荷跳闸而导致用户停电；不破坏系统的稳定性，不出现电压崩溃等事故。

广度优先搜索与深度优先搜索

广度优先搜索与深度优先搜索是两种针对图、树常用的搜索算法，前者的实现原理是利用queue的特性,其算法思想被称为“分枝定界”，后者的实现原理是利用stack的特性，其算法思想被称为回溯(backtracking)，下面我们以数组定义的简化模型来实现这两种算法。

假设我们用数组定义了一个迷宫，要找这个数组中两点之间的路径，比如{0,0}和{9,9}。

char board[MAZE_SIZE][MAZE_SIZE] = {
        {0,1,1,1,1,1,0,0,0,0},
        {0,0,0,0,0,1,0,1,0,0},
        {0,0,0,1,0,1,0,0,0,0},
        {0,1,0,1,0,1,0,1,1,0},
        {0,1,0,1,0,1,0,1,0,0},
        {0,1,1,1,0,1,0,1,0,1},
        {0,1,0,0,0,1,0,1,0,1},
        {0,1,0,1,1,1,0,1,0,0},
        {1,0,0,0,0,0,0,1,0,0},
        {0,0,0,0,1,1,1,1,0,0}};

首先我们定义一个Step函数，在某个point上的某个方向试图走出一步，如果能走则返回true，否则返回false。

bool Step(Position& pos, int& dir)
    {
       int offsetx[DIRECTION] = {1,0,-1,0};
       int offsety[DIRECTION] = {0,-1,0,1};
       dir = dir%DIRECTION;

       int tempx = pos.x + offsetx[dir];
       int tempy = pos.y + offsety[dir];

       if(tempx<0 || tempx>=MAZE_SIZE || tempy<0 || tempy>=MAZE_SIZE
           || board[tempy][tempx]==1)
           return false;

       pos.x = tempx;
       pos.y = tempy;
       return true;
    }

广度优先是将与当前位置相邻且尚未遍历的point push进queue中，然后不停的将queue中的element pop出来重复前面的动作，这样就使得跟起诉位置越近的点越先处理，能找出一条两点之间最短的路径。

    bool WFS(Position begin, Position& end)
    {
       std::queue<Position> posQueue;
       posQueue.push(begin);
       while(!posQueue.empty())
       {
           Position pos = posQueue.front();
           if(pos == end)
              return true;
           board[pos.y][pos.x] = 1;

           int dir=0;
           while(dir < DIRECTION)
           {
              pos = posQueue.front();
              if(Step(pos, dir))
                  posQueue.push(pos);
              dir++;
           }
           posQueue.pop();
       }
       return false;
    }

深度优先是将与当前point相邻的某个element push进stack中，直到找不到要寻找的点才将stack中的element pop出来，再从该element其他方向的相邻element中寻找

 bool DFS(Position begin, Position end)
    {
       std::stack<Position> posStack;
       Position pos, lastpos;
       pos = begin;
       while(pos.x!=end.x || pos.y!=end.y)
       {
           lastpos = pos;
           int dir=0;
           while(dir < DIRECTION)
           {
              if(Step(pos, dir))
                  break;
              dir++;
           }

           if(!(pos==lastpos))
           {
              board[pos.y][pos.x] = 1;
              posStack.push(lastpos);
           }
           else
           {
              if(posStack.empty())
                  return false;
              pos = posStack.top();
              posStack.pop();
           }
       }

       return true;
    }

递归和stack的实现有着类似的逻辑，而且可以写的更加简洁:

bool Recursion(Position pos, Position& end)
    {
       if(pos == end)
           return true;

       Position cur = pos;
       board[pos.y][pos.x] = 1;
       int dir=0;
       while(dir < DIRECTION)
       {
           pos = cur;
           if(Step(pos, dir) && Recursion(pos, end))
              return true;
           dir++;
       }
       return false;
    }

若干笔记……